


Notes on Semi-Rigid Connections
Dr. John McGuire - July 6, 1995
Formerly of the Goddard Space Flight Center
Contact: Jim Loughlin - NASA Goddard Space Flight Center
One of the basic assumptions of conventional structural analysis is that joints are either perfectly rigid or perfectly hinged. Therefore, when analyzing a structure, joints are idealized as either fixed or hinged. However, in actual structures, typical connections do not behave in either a perfectly rigid or a perfectly hinged manner. The different types of connections that are commonly used fill the entire flexibility spectrum from flexible "hinge like" connections to semi-rigid connections to rigid connections. These non-ideal connections are often referred to as flexible connections, semi-rigid connections, spring hinged joints, or sticky hinges.
To achieve a more accurate analysis of a structure it would be advantageous to include the true behavior of the joints. For example, there is a substantial variation in the distribution of bending moment for a beam with hinged, semi-rigid, and fixed joints (Figure 1). (W = force/unit length)
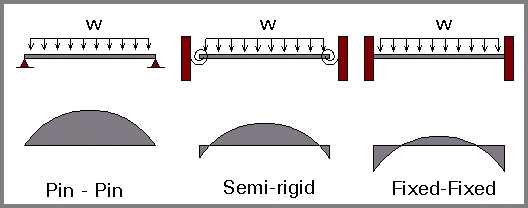
Figure 1 - Moment Diagrams for Uniform Loading
There is also a substantial difference in the minimum natural frequency and mode shape of a beam with hinged, semi-rigid, and fixed joints (Figure 2).
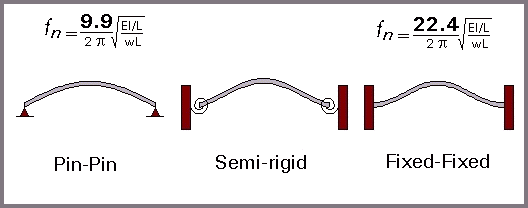
Figure 2 - Minimum Natural Frequency for Beams of Uniform Mass
E = Young's Modulus; I = moment area of inertia; L = length of beam; W = force/unit length
Semi-rigid joints can be modeled using a rotational spring which separates a member from it's surrounding environment. The rotational spring is characterized by it's moment-rotation curve, where the rotational stiffness of the spring k is equal to the slope of the moment-rotation curve (Figure 3}. The value of k for a given connection detail can be determined by testing.
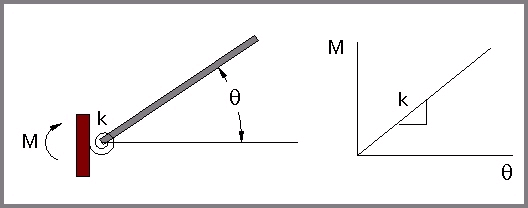
Figure 3 - Moment-Rotation Relation for a Rotational Spring
The magnitude of the stiffness of the spring hinge k does not determine if a joint will behave in a rigid or flexible manner. Rather it is the ratio of the spring stiffness k to the flexural stiffness of the member EI/L that determines what behavior will be exhibited. This ratio is often called the "joint stiffness" and is defined as kL/EI.
In order to visualize this phenomenon consider some "medium sized" spring with spring stiffness K-medium (Figure 4). If a very flimsy, spaghetti-like member is connected to it, even though the spring is only "average sized" it will still keep the flimsy member from rotating at the support, just like a rigid connection would. However, if a very stiff member were connected to our "average sized" spring, it would appear as if the spring had little to no effect in restraining the member.
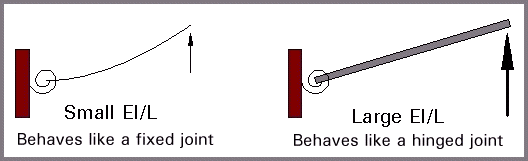
Figure 4 - Same Spring - Different Behavior
This now raises the question of what specific values of the stiffness ratio will result in hinged behavior, semi-rigid behavior, or fixed behavior. To answer this question the dynamic and static behavior of a prismatic beam with uniform load was investigated.
A finite element model of a typical sized beam with spring hinges at the supports was created (Figure 5 inset). A NASTRAN normal modes analysis was performed to obtain the minimum natural frequency for various values of the spring stiffness k. The results of this analysis are shown in Figure 5.
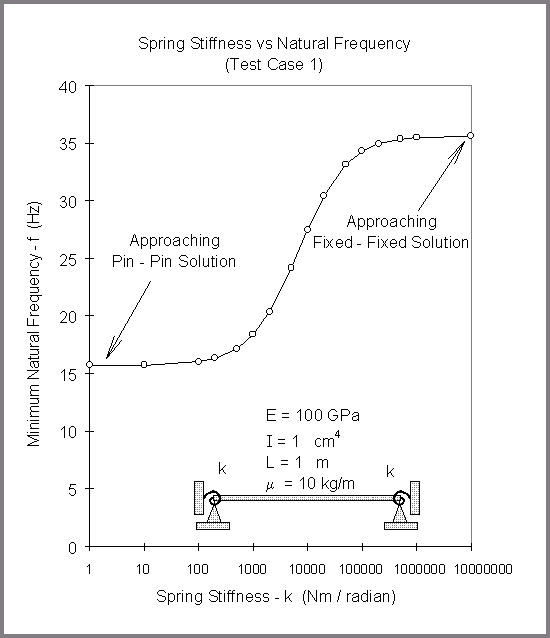
Figure 5
As k gets smaller the solution approaches the pin-pin solution. as k gets larger the solution approaches the fixed-fixed solution. Furthermore, there is a discernable range in which the behavior changes from pined to fixed.
The results shown in Figure 5 are for a specific beam. For the results to be of use they must be applicable to any beam. Therefore, the behavior of a second beam with increased mass (100 times greater than the initial test case) and the behavior of a third beam with increased flexural stiffness (100 times greater than the initial test case) was investigated, the results are shown in Figure 6.
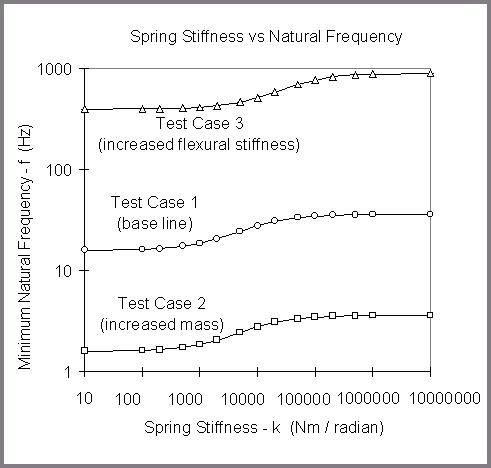
Figure 6
When the mass was increased the natural frequency dropped but the transition range remained the same. Therefore it appears that the mass has no effect on the joint stiffness. When the flexural stiffness was increased the natural frequency increased and the transition range shifted also, demonstrating that the flexural stiffness of the beam effects the joint stiffness.
The previous results can be non-dimensionalized. The natural frequency can be non-dimensionalized using the natural frequency of the pin-pin case as zero and the natural frequency of the fixed-fixed case as 1. And instead of the spring stiffness the joint stiffness ratio of K/ EI/L will be used. The results plotted in this manner are shown in Figure 7.
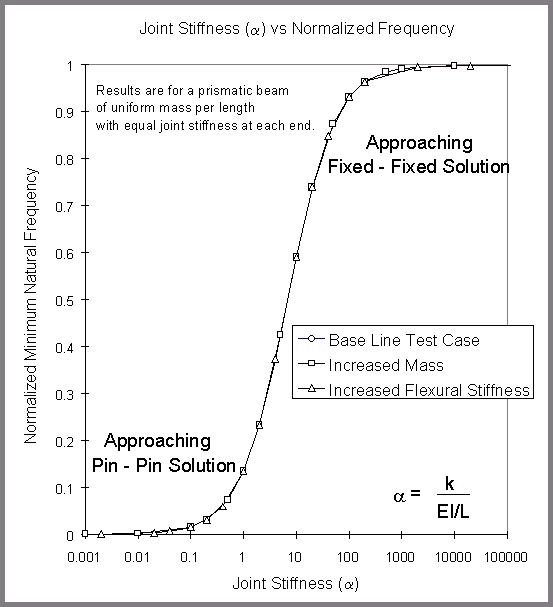
Figure 7
When plotted in this manner all three test cases fall on the same line. From this it can be seen that if the joint stiffness is less than 1 the natural frequency is within 10% of the pin-pin condition and if the joint stiffness is greater than 100 the natural frequency is within 10% of the fixed-fixed condition.
Conclusion
Rotational springs can be used to model semi-rigid restraint conditions. The restraint conditions can be characterized by a quantity called the joint stiffness. The joint stiffness depends on the ratio of the spring stiffness k to the flexural stiffness EI/L of the beam and is defined as kL/EI. NASTRAN analysis results confirm that the mass of a beam does not effect the joint stiffness, only the flexural stiffness of the beam does.
It was also found that when the joint stiffness is less than 1.0 the beam behaves as if it is hinged, while if the joint stiffness is greater than 100 the beam behaves as if it is fixed. Therefore it may not be worth the effort to model a connection with a rotational spring if the resulting joint stiffness being used is less than 1 or greater than 100. Furthermore, if semi-rigid behavior is desired a joint stiffness between 1 and 100 should be used. Figure 7 can help in determining what joint stiffness should be to used to achieve a particular behavior.
Written by Dr. John McGuire