The Craig-Bampton Method

Scott Gordon
NASA Goddard Space Flight Center
May 6, 1999

(updated January 2008)

I. Background

Who is Craig Bampton?
Coupling of Substructures for Dynamic Analysis
by Roy R. Craig Jr. and Mervyn C. C. Bampton
AIAA Journal, Vol. 6, No. 7, July 1968
(Link is to a Word document directly from Mr. Craig's website)

What is the Craig-Bampton Method?

• Method for reducing the size of a finite element model.
  
• Combines motion of boundary points with modes of the structure assuming the boundary points are held fixed.
  
• Similar to other reduction schemes

Guyan Reduction

Modal Decoupling

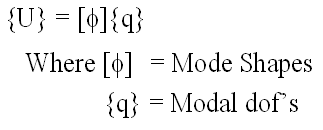
Craig-Bampton

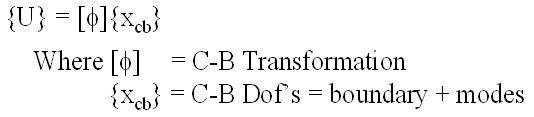
Why is the C-B Method Used?
• Allows problem size to be reduced
• Accounts for both mass and stiffness (unlike Guyan reduction)
• Problem size defined by frequency range
• Allows for different boundary conditions at interface (unlike modal decoupling)
   
  
• Example Problem Model (see below)

II. Craig-Bampton Theory

• Equation of motion (ignoring damping)

(1)

• The Craig-Bampton transform is defined as:

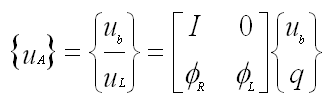(2)

Where:
 
u_b = boundary DOFs
u_L = internal (leftover) DOFs
= rigid body vector
= fixed base mode shapes
q = modal DOFs
The 2 X 2 matrix in Equation 2 is the Craig-Bampton transformation matrix.
• Combining equations (1) and (2) and pre-multiplying by

(3)

• Define the C-B mass and stiffness matrices as

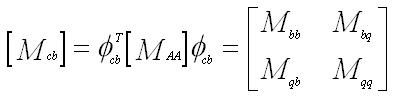	(4)
	(5)

• Write equation (3) using equations (4) and (5)

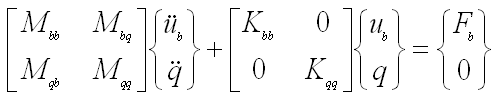(6)

where input forces are applied at the boundary only (F = 0).
• Important properties of the C-B mass and stiffness matrices
  • M_bb = Bounday mass matrix -- total mass properties translated to the boundary points

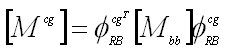
  (7)

  • K_bb = Interface stiffness matrix -- stiffness associated with displacing one boundary DOF while other are held fixed
        - If the boundary point is a single grid (i.e. non-redundant) then
          K_bb = 0

  • If the mode shapes have been mass normalized (typically they are) then

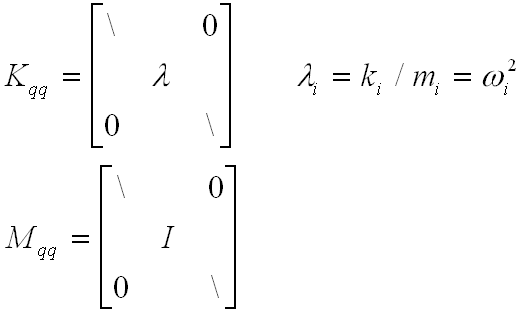(8)

• We can finally write the dynamic equation of motion (including damping) using the C-B transform as

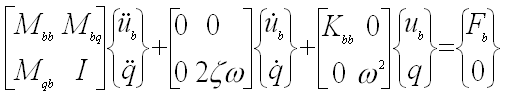(9)

where = modal damping ( = % critical)
• Summary of C-B Theory
  • C-B Mass and Stiffness Matrices fully define system
    
  • Dynamics problem solved using C-B DOFs
    
  • C-B boundary DOFs provide location to apply BC’s and Forces or to couple with another structure
    
  • C-B transform is used to calculate physical responses from C-B responses

III. How to Create a C-B Model

  $ C-B Output File
ASSIGN,OUTPUT4='cb_ex1.kmnp',STATUS=unknown,UNIT=31
ID GORDON,CB_EX1
  $  Normal Modes Solution
SOL SEMODES
TIME 5
DIAG  8,14
  $ C-B DMAP
INCLUDE 'path/cb103_2005r2b.dmp'
CEND
$
TITLE = Craig-Bampton Example 1
ECHO = NONE
METHOD = 1
$  SPC = 1
  $ Request modal effective mass output
  MEFFMASS(ALL) = YES
$
  $ Request Output Grid Point Forces, Element Forces, and Element Stresses
  $ This is recovered in the .F06 file
SET 100 = 209,210
SET 101 = 110,114
GPFORCE = 100
ELFORCE = 101
ELSTRESS = 101
$
BEGIN BULK
$
PARAM,AUTOSPC,YES
PARAM,GRDPNT,0
PARAM,WTMASS,0.00259
$
  $ Print G-set (U1 in the DMAP) & R-set internal order
PARAM,USETSEL,0
PARAM,USETSTR1,U1
PARAM,USETSTR2,R
PARAM,USETPRT,0
$
$ Acceleration Output
  $ Recover accleration response at GRID 11
  $ This is output in the .kmnp file and processed in FLAME
USET1	U1	123456	11
$
  $ Define number of modes to recover (or frequency range)
EIGRL          1                      10       0                    MASS
$
  $ Boundary (R-set) Defined on SUPORT cards 
  $  1 boundary point x 6 DOFs 
  $  = 6 physical boundary points 
SUPORT	999	123456
SPC            1     999  123456      0.
$
  $ 7) Don't forget the rest of your bulk data 
INCLUDE 'bulkdata'
$
ENDDATA

What is created?

• file cb_ex1.kmnp which contains C-B stiffness and mass matrices (k,m), net CG ltm (n), and the C-B transformation matrix (phi_g)
• .kmnp file is in NASTRAN binary output4 format
• K and M size is [C-B DOFs (boundary + modal) x C-B DOFs]
• phi_g size is [G-set rows x C-B DOFs]
• Net CG LTM recovers CG accelerations and I/F Forces, Size is [6+boundary DOFs x C-B DOFs]

How do you use this?

• Solve dynamics problem for C-B DOF response using the K and M matrices
• Transform C-B responses using phi_g to get physical responses

IV. Load Transformation Matrices (LTMs)

• LTM is a generic term referring to the matrix used to transform from C-B DOFs to physical DOFs (also referred to at OTMs, ATMs, DTMs …)
• In its simplest form, the LTM is simply the phi_g matrix

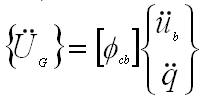(10)

(Only the rows corresponding to the physical DOFs of interest are needed)

• There are other useful LTMs that can be created
  • Interface (I/F) forces
    
  • Net CG accelerations
    
  • Stress and force LTMs

• I/F Force LTM (created by C-B DMAP)
  I/F Force =

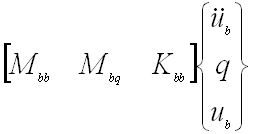(11)

(If boundary is non-redundant, then K_bb = 0)

• Net CG LTM (created by C-B dmap)
  Net CG acceleration =

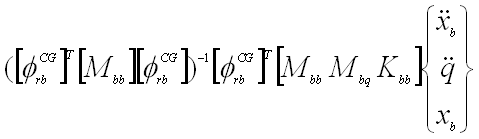(12)

where = mass matrix about CG (6 X 6)
and = rigid body transform from I/F to CG (BDOF X 6)

• PHIZ LTM
  • Allows physical displacements to be calculated from C-B accelerations:

(13)

• Same as modal acceleration approach in NASTRAN
  
• Useful in calculating relative displacements between DOFs
  
• Also used to calculate stresses and forces which are a function of displacements
  
• Calculated from C-B dmap using PARAM,PHZOUT,1

• LTM’s can be created using FLAME, MATLAB or using DMAP
• LTM’s can (and usually do) contain multiple types of responses

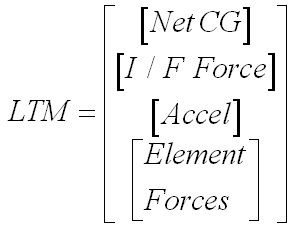(14)

• LTM’s can be used to recover responses for nested C-B models

(15)

where = row partition of CB₁ DOFs from the CB₀ PHI_G matrix

• Creating LTMs - See example file below for a sample FLAME script for creating an LTM

V. Checking C-B Models AND LTMs

• C-B Models and LTMs should be verified to make sure that they have been created correctly (especially for complicated LTM’s or nested C-B models)
• C-B Mass and stiffness matrices can be checked by computing free-free and fixed-base modes
• C-B boundary Mass matrix can be transformed to CG and compared with NASTRAN GPWG
• LTMS can be checked by applying unit acceleration at the boundary:

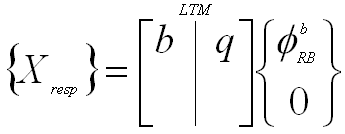(16)

where = boundary rigid body vector (b X 6)
• Each response column represents acceleration in a single direction
  
• Accelerations should be in correct directions
  
• Forces should recover weight or correct moments
  
• Unit acceleration applied to PHI_Z can be checked by gravity run with physical model and comparing displacements

VI. Example and Files

• Following are links to the Craig-Bampton DMAP as well as a C-B example:
  • cb103_2005r2b.dmp — DMAP for creating a C-B model in MSC Nastran v.2005r2b (REMOVED FOR ITAR REASONS)
  • cb_pres2.ppt — Scott's Powerpoint presentation on the C-B method (160KB)
  • Primer_on_the_Craig-Bampton_Method.pdf — John Young's Primer on all things Craig-Bampton (2MB)
  • C-B_example.zip — Example files for creating a C-B model and the load transformation matrix (LTM) in MSC Nastran v.2005r2b
    (16MB - includes the above files and the Craig-Bampton paper) (REMOVED FOR ITAR REASONS)

Scott Gordon

Home 
» Back to the Book « 
Presentations 
References 
Workshop 
Links 
FEMCI Is 

 
- NASA GSFC 
- GSFC Code 542